IL PENDOLO SEMPLICE

  

Scopo dell'esperimento. Determinare il periodo di oscillazione di un pendolo semplice. Applicare le nozioni sugli errori di una grandezza fisica. Trovare sperimentalemente in che modo il periodo di un pendolo dipende dalla sua lunghezza. Determinare il valore dell'accelerazione di gravità.

 

Premessa. Un pendolo semplice è una piccolo pesetto vincolato ad un sostegno per mezzo di un filo flessibile, inestensibile e di massa trascurabile. La posizione d’equilibrio del pendolo è quella nella quale il centro di sospensione, il filo teso, e il centro del pesetto sono allineati lungo la verticale. Se si allontana il pesetto dalla posizione di equilibrio lasciandolo libero, esso inizia ad oscillare attorno a questa posizione. Il periodo del pendolo è il tempo che esso impiega a compiere una oscillazione completa, cioè a tornare nella posizione da cui è partito e nelle stesse condizioni di movimento. Se l’angolo di apertura dell’oscillazione è piccolo (minore di circa 5 gradi), il moto del pendolo può essere considerato un moto armonico semplice. Pertanto, è facile dimostrare che il periodo T è dato dalla relazione:

dove L è la lunghezza del pendolo e g è l'accelerazione di gravità, che racchiude le quattro leggi del pendolo:

1^a Le piccole oscillazioni si compiono nello stesso tempo (sono isocrone), indipendentemente dall’ampiezza.

2^a Il periodo non dipende dalla massa del pesetto.

3^a Il periodo è direttamente proporzionale alla radice quadrata della lunghezza L del pendolo

4^a Il periodo è inversamente proporzionale alla radice quadrata dell’accelerazione di gravità g.

Dalla (1) si ricava che:

 

Pertanto il pendolo semplice consente una misura facile  e sufficientemente precisa dell’accelerazione di gravità.

 

 Materiale occorrente. Asta lunga. Morsetto doppio. Cronometro meccanico, sensibilità 1/10 s. Riga millimetrarta da 1 m o rotella metrica millimetra da 2 m. Un pesetto con gancio o un dado di ferro da bullone. Cordicella sottile in cotone lunga circa 1 metro.

.

Esecuzione dell'esperimento. Per realizzare un pendolo semplice basta  sospendere un pesetto a un filo non elastico. Se si utilizza un morsetto doppio è possibile annodare il filo del pendolo a una delle viti del morsetto, oppure, realizzare una sospensione bifilare come mostrato nella figura; in questo modo si evitano le orbite ellittiche della massa pendolare sospesa ad un unico filo. La misurazione della lunghezza del pendolo, che può essere eseguita partendo dalla gola del morsetto, nella quale è posto il filo, fino al  centro del dado, è di solito abbastanza precisa. Infatti , se la riga è ben allineata con il filo, si può ammettere di fare un errore di non più di mezzo centimetro nel valutare la lunghezza del pendolo con un errore percentuale, per un pendolo lungo 1 metro, sempre inferiore all’1%. Invece nella misura di un singolo periodo l’errore percentuale sarebbe dieci volte più elevato perché, ad esempio, su un periodo di 2 s c’è un’incertezza di ± 0.2 s (0.1 s dovuto allo strumento e altrettanto dovuto ai riflessi del cronometrista). Pertanto è necessario misurare la durata di almeno dieci oscillazioni complete.  Il periodo è uguale a 1/10 del tempo segnato dal cronometro ipotizzando, come mostra la (1), che ciascuna oscillazione ha la stessa durata. In questo modo l’incertezza su T, che rimane sempre di ± 0.2 s, si distribuisce su 10 periodi, rendendo l’incertezza sul singolo periodo 10 volte più piccola.

 

L’istogramma della dispersione dei periodi attorno al valore medio. Comunicare al pesetto un piccolo spostamento e far scattare il cronometro quando la pallina si trova all’estremità dell’arco di traiettoria percorsa, cioè all’atto di invertire la marcia, e dopo aver contato 10 oscillazioni complete fermare il cronometro. Inserire il valore ottenuto in una tabella dove nella prima colonna è indicato il numero progressivo della misura. La seconda colonna contiene la durata t delle 10 oscillazioni e la terza il periodo calcolato, T= t/10; riportare il valore di T arrotondato con due cifre dopo la virgola. Ripetere poi questa misura per almeno trenta volte mantenendo costante la lunghezza del pendolo. Organizzare la serie dei valori di periodo ottenuti in un istogramma nel seguente modo: a) individuare il valore minimo e massimo dei periodi  b) suddividere l’intervallo avente come estremi il minimo e il massimo periodo in un numero di sottointervalli piccolo a confronto del numero totale delle misure, ad esempio 6-7   c) contare il numero delle misure comprese in ciascun intervallo e costruire il diagramma d) verificare che le misure si addensano attorno al valore medio e) stabilire che la forma dell’istogramma cambia al variare del numero dei sottointervalli   f) determinare la deviazione standard.

 

La dipendenza dalla lunghezza e la determinazione dell’accelerazione dei gravità. Determinare il periodo del pendolo riducendo di volta in volta la sua lunghezza, da quella massima fino a circa 20 cm, facendo comunque in modo da ottenere almeno 10 misure. Per ogni valore della lunghezza L ripetere la misura del periodo per confermare il valore precedentemente ottenuto. Riportare i valori di T e L in una tabella, e poi in un grafico e verificare che la curva interpolatrice non è una retta. Riportando i valori su un grafico (T²;L) si dovrebbe trovare una retta che conferma la proporzionalità diretta fra la lunghezza del pendolo e il suo periodo elevato al quadrato. Utilizzando il grafico (T²;L) e calcolando la pendenza della retta, è possibile ricavare il valore dell'accelerazione di gravità. La linearizzazione proposta non è l’unica possibile. Ad esempio, linearizzare per mezzo dei logaritmi, senza tener conto della (1), vale a dire ipotizzando una dipendenza di tipo potenza di T da L, cioè della forma T = kLⁿ e determinare il valore di n come pendenza della retta in un diagramma ln T-ln L. Verificare che  n »0,5.

 

Esempio di misure

 

Elaborazione statistica delle misure del periodo di un pendolo semplice. Sono presentate alcune elaborazioni, eseguite con le calcolatrici grafico-simboliche Texas Istruments TI-89  e TI-92 Plus, della misura del periodo di un pendolo semplice. Le misure sono state effettuate dai corsisti della SILSIS che hanno misurato N volte dieci oscillazioni complete  con un cronometro avente un sensibilità di 0,1 s; i periodi sono stati ottenuti dividendo il valore misurato per 10. Le videate delle calcolatrici mostrano l'istogramma e i risultati statistici. Nell'istogramma la larghezza di ciascuna colonna è pari a 0.01 s mentre sulle ordinate è indicato quante volte si è ottenuto un certo valore di periodo, cioè la frequenza assoluta.

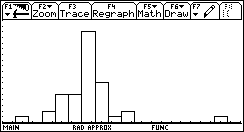
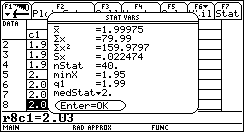
40 misure del periodo di un pendolo semplice lungo 99 cm, elaborazione TI-92 Plus

scarica i dati in Excel pendolo40.xls

 30 misure del periodo di un pendolo semplice lungo 92 cm, elaborazione TI-89

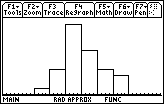
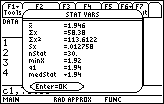
scarica i dati in Excel pendolo30.xls

 

 

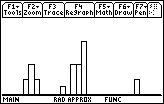
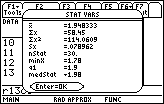
30 misure del periodo di un pendolo semplice lungo 94 cm, elaborazione TI-89

 

Si può esservare che delle tre serie di misure la più precisa è la seconda perchè i suoi valori sono più addensati attorno al valore medio e questo è messo in evidenza nella relativa videata dei risultati statistici, dove, la deviazione standard (Sx) ha il valore più basso, circa  0.01 s. L'alto valore della deviazione standard nell'ultima serie di misure (=0.08 s) e l'irregolarità del suo istogramma indicano misure di bassa precisione e affette da errori sistematici.